Introduction to Exploratory Data Analysis (EDA)

Exploratory Data Analysis (EDA) is the crucial first step in the data analysis process. Before applying complex statistical models or machine learning algorithms, it is essential to understand the structure, trends, and peculiarities of the data you are working with. In this introductory section, we will explore the fundamental concepts of EDA and its role in data analysis.

Importance of EDA

EDA serves several purposes:

Understanding Data: EDA helps us become familiar with the dataset, identify the available variables, and understand their nature (numeric, categorical, temporal, etc.).
Detecting Patterns: EDA allows us to detect patterns, relationships, and potential outliers within the data. This is critical for making informed decisions during the analysis.
Data Cleaning: Through EDA, we can identify missing values, outliers, or data inconsistencies that require cleaning and preprocessing.
Feature Engineering: EDA may suggest feature engineering opportunities, such as creating new variables or transforming existing ones to better represent the underlying data.
Hypothesis Generation: EDA often leads to the generation of hypotheses or research questions, guiding further investigation.
Communicating Insights: EDA produces visualizations and summaries that facilitate the communication of insights to stakeholders or team members.

In the following sections, we will delve into the practical aspects of EDA, starting with data simulation and visualization techniques.

Generating Simulated Data

Before diving into Exploratory Data Analysis (EDA) on real datasets, it’s helpful to begin with the generation of simulated data. This allows us to have full control over the data and create example scenarios to understand key EDA concepts. In this section, we will learn how to generate simulated datasets using R.

Parameters and Variables

To start, let’s define some basic parameters that we’ll use to generate simulated data:

x_min: The minimum value for the variable x.
x_max: The maximum value for the variable x.
x_step: The increment between successive x values.
y_mean: The mean value for the dependent variable y.
y_sd: The standard deviation for the dependent variable y.
y_min: The minimum possible value for y.
y_max: The maximum possible value for y.

We will use these parameters to generate sample data.

Now, let’s proceed to generate sample data based on the defined parameters. In this example, we’ll create a simple dataset with the following variables:

x: A sequence of values ranging from x_min to x_max with an increment of x_step.
var_random: A random variable with values uniformly distributed between y_min and y_max.
var_norm: A variable with values generated from a normal distribution with mean y_mean and standard deviation y_sd.
var_sin: A variable with values generated as the sine function of x.

Here’s the R code to create the sample dataset:

library(data.table)

# Parameters
x_min   <- 0
x_max   <- 10   
x_step  <- 0.01

y_mean  <- 0.5
y_sd    <- 0.25
y_min   <- -1
y_max   <- 1     

x       <- seq(x_min, x_max, x_step)

# Variables
var_random  <- runif(length(x), y_min, y_max)
var_norm    <- rnorm(length(x), y_mean, y_sd) 
var_sin     <- sin(x)

# Data.frame 
df  <- data.frame(x, var_random, var_norm, var_sin)
dt  <- data.table(df)

# Melt 
dtm <- melt(dt, id.vars="x")

This code creates a dataset df and a data.table dt containing the generated variables. The melt function from the data.table library is used to reshape the data for visualization purposes.

With our simulated data ready, we can now move on to creating various plots and performing EDA.

In this section, we will explore various visualization techniques that play a crucial role in Exploratory Data Analysis (EDA). Visualizations help us gain insights into the data’s distribution, patterns, and relationships between variables. We will use the simulated dataset generated in the previous section to illustrate these techniques.

Choosing the Right Plot

The choice of visualization depends on the nature of your data and the specific aspects you want to highlight. Generally, in EDA, we often need to:

Examine Changes Over Time: Use time series plots when you want to assess changes in one or more variables over time.
Check for Data Distribution: Create distribution plots, such as histograms and density plots, to understand how data points are distributed.
Explore Variable Relationships: Employ correlation plots and scatter plots to identify linear relationships between variables.

Let’s start by examining these aspects one by one using our simulated dataset.

Time Series Plots

To explore changes over time, we’ll create a time series plot for the var_sin variable. This variable represents a sine wave and is well-suited for a time series representation. Here’s the R code to create a time series plot:

library(ggplot2)

Warning: il pacchetto 'ggplot2' è stato creato con R versione 4.3.3

p <- ggplot(dtm[variable == "var_sin"], aes(x = x, y = value, group = variable)) +
     geom_line(aes(linetype = variable, color = variable))
p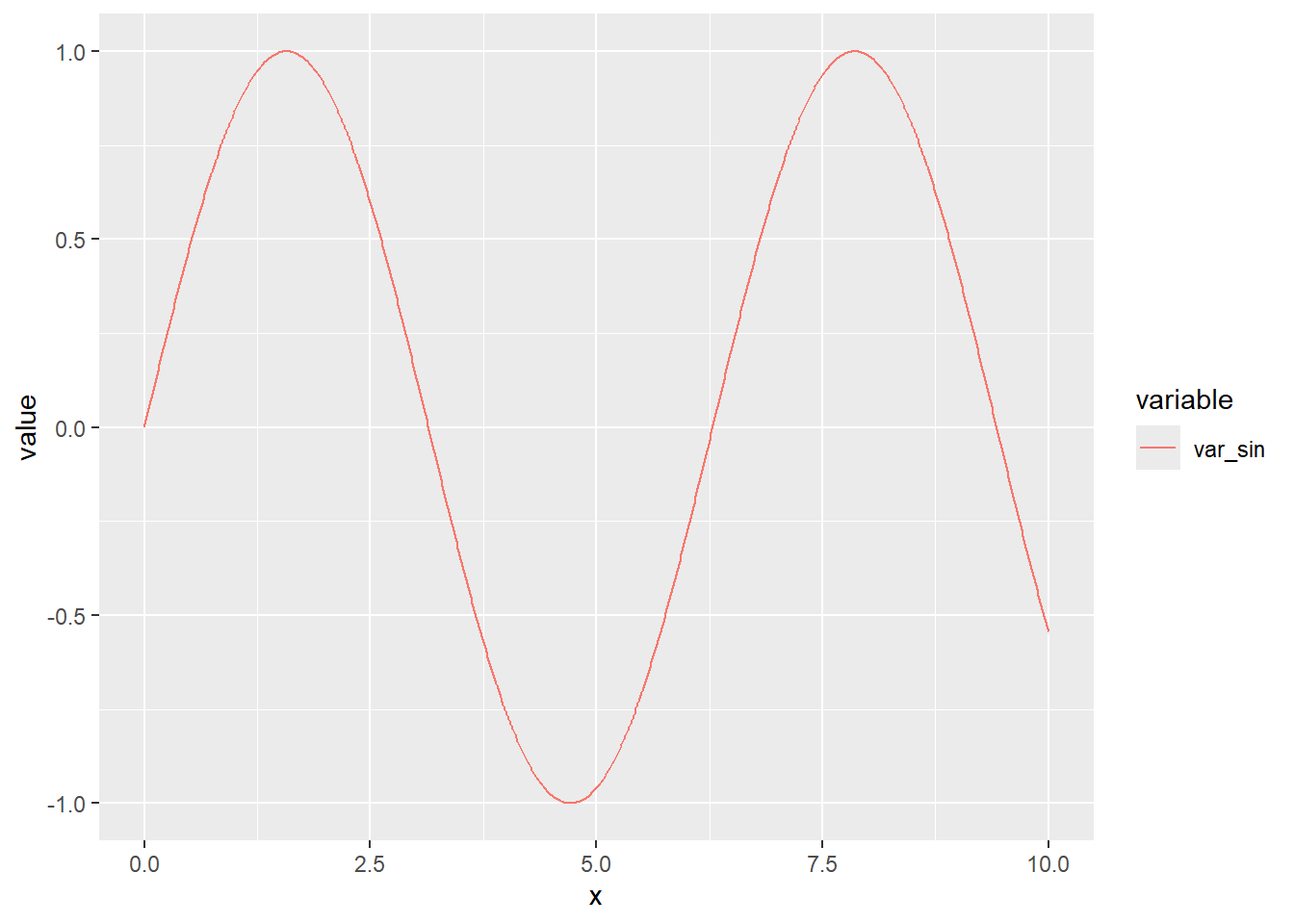

In this code, we use ggplot2 to create a line plot for the var_sin variable.

Distribution Plots

To check the data distribution, we’ll create histogram plots for each of the variables: var_random, var_norm, and var_sin. Histograms provide a visual representation of the frequency distribution of data values. Here’s the R code:

p3 <- ggplot(dtm[variable == "var_sin"], aes(y = value, group = variable)) +
     geom_histogram(bins = 20) 

p4 <- ggplot(dtm[variable == "var_norm"], aes(y = value, group = variable)) +
     geom_histogram(bins = 20) 

p5 <- ggplot(dtm[variable == "var_random"], aes(y = value, group = variable)) +
      geom_histogram(bins = 20)
p3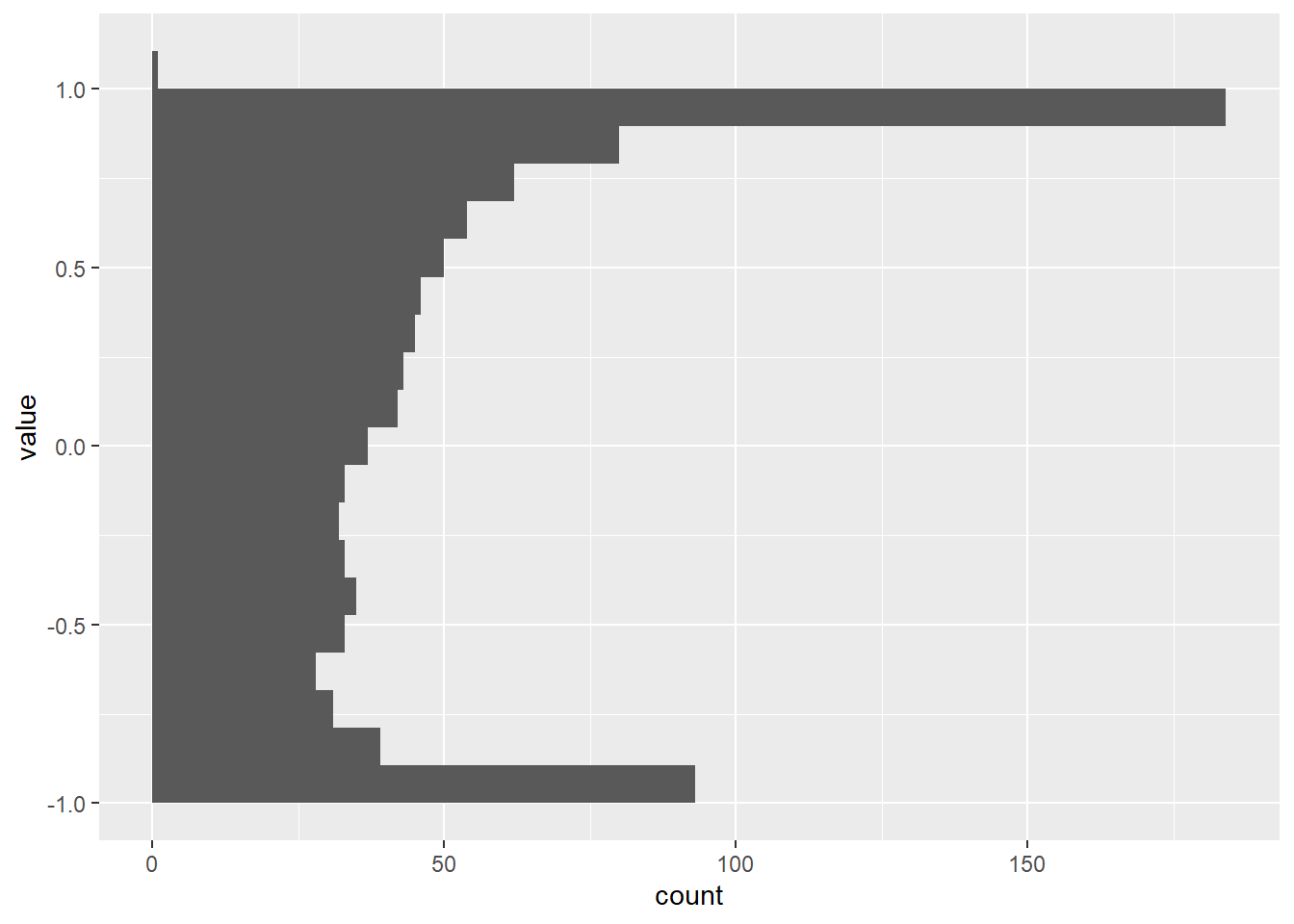

p4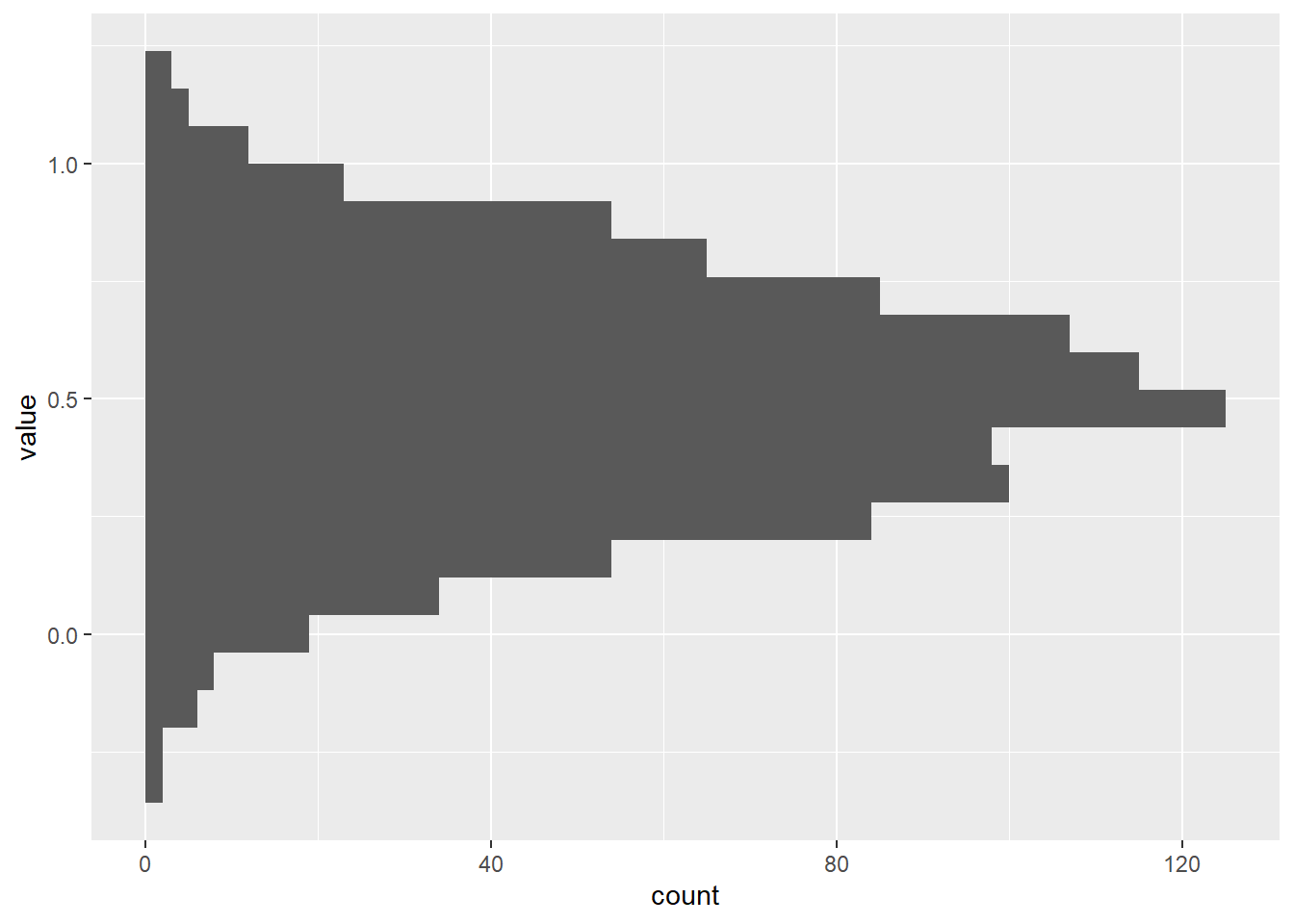

p5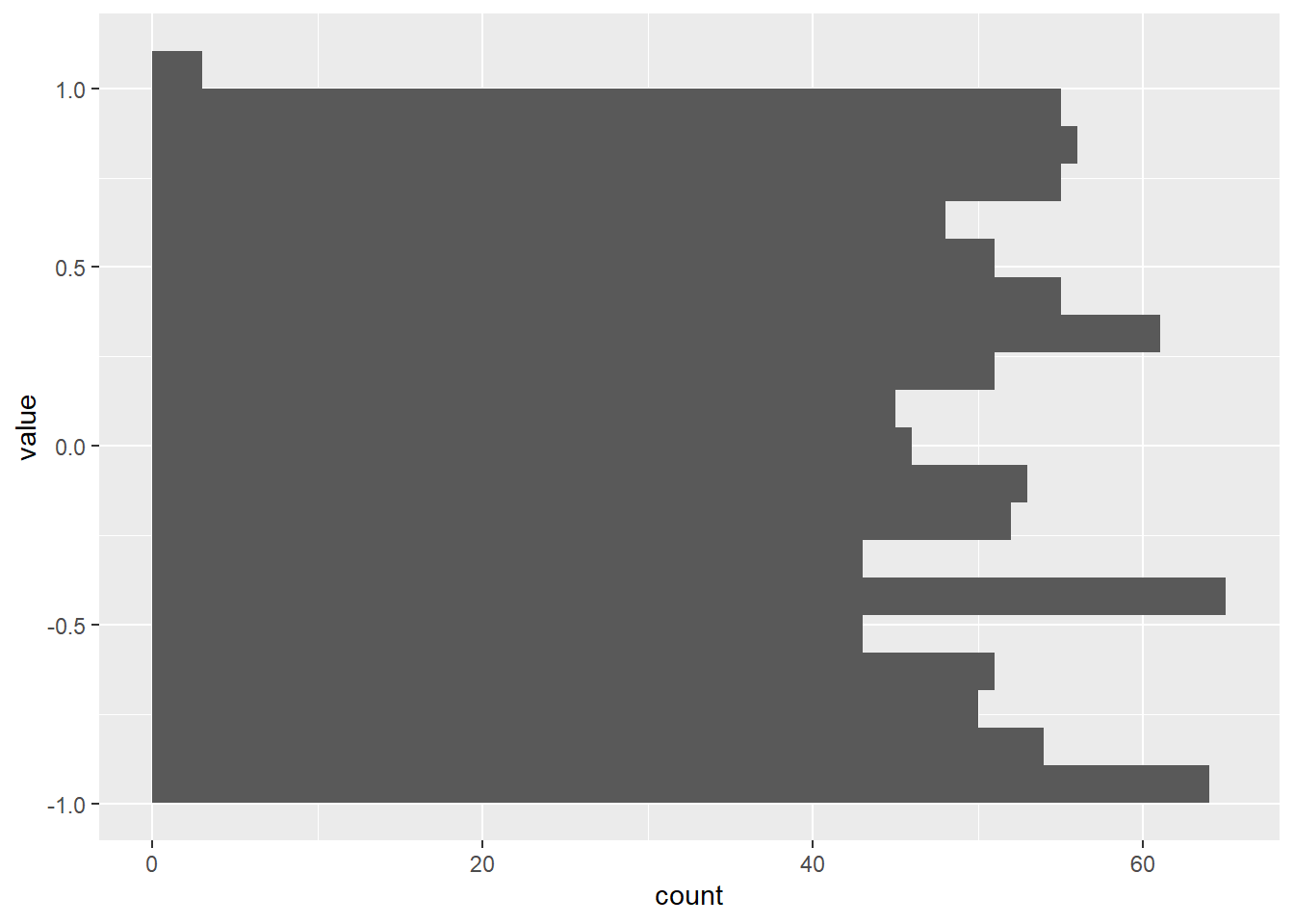

These plots will help us understand the distribution characteristics of our variables.

Correlation Plots

Correlation plots allow us to examine relationships between variables. We’ll create scatter plots for pairs of variables to assess their linear correlation. Here’s an example for var_sin and var_sin2:

options(repr.plot.width = 7, repr.plot.height = 7)

var_random2  <- runif(x,y_min,y_max)
var_norm2    <- rnorm(x,y_mean,y_sd) 
var_sin2     <- sin(x) + rnorm(x,0,0.01) 

df2<- data.frame(df,var_sin2,var_norm2,var_random2)
dt2 <- data.table(df2)

p10 <- ggplot(dt2) + geom_point(aes(x = var_sin, y = var_sin2)) 
p10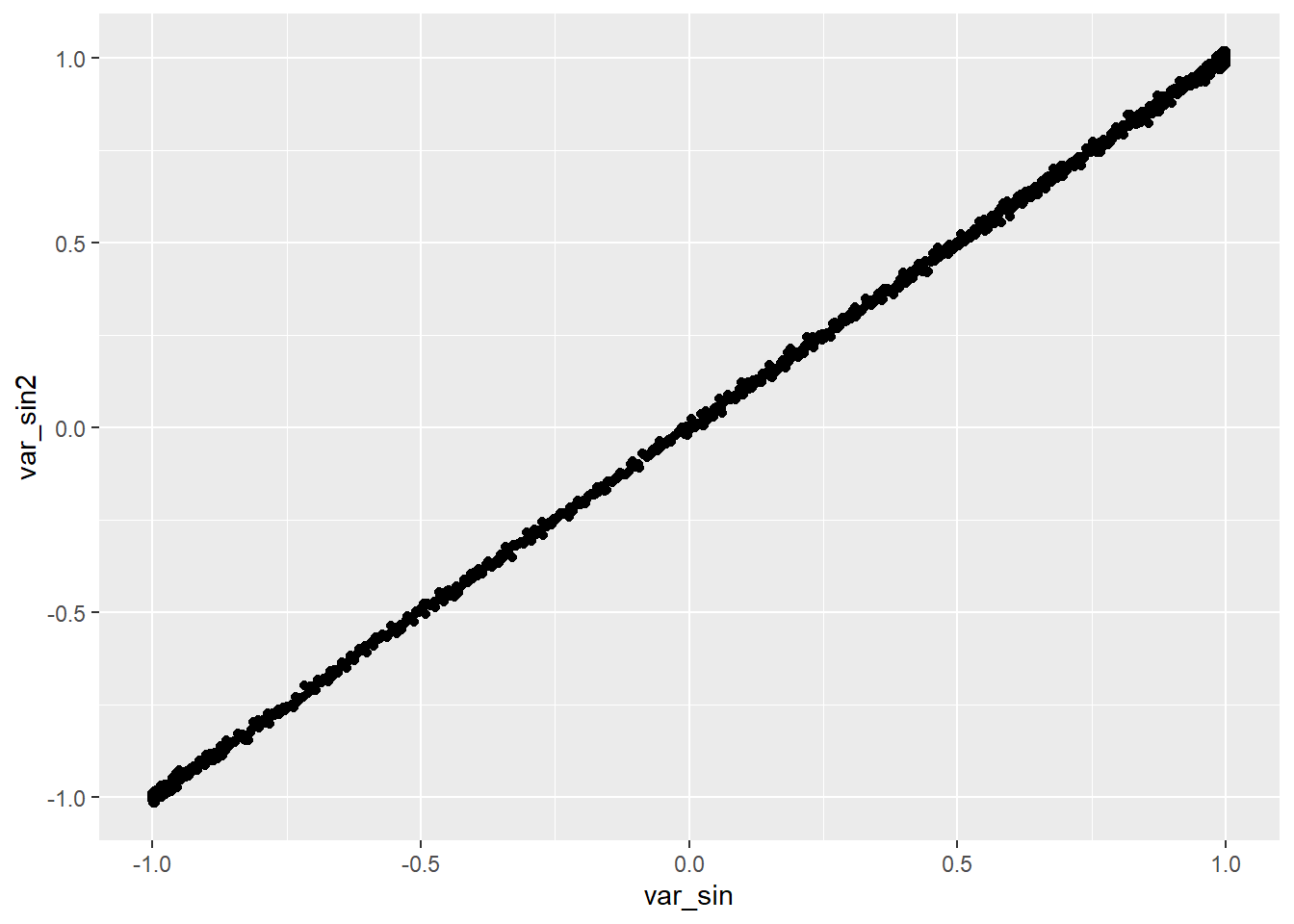

These scatter plots help us identify whether variables exhibit linear correlation.

In the following sections, we’ll delve deeper into each of these plot types, interpret the results, and explore additional visualization techniques for EDA.

Box Plots

Box plots, also known as box-and-whisker plots, provide a summary of the data’s distribution, including median, quartiles, and potential outliers. They are particularly useful for comparing the distributions of different variables or groups. Here’s an example of creating box plots for var_random, var_norm, and var_sin:

p6 <- ggplot(dtm, aes(x = variable, y = value)) +
      geom_boxplot()
p6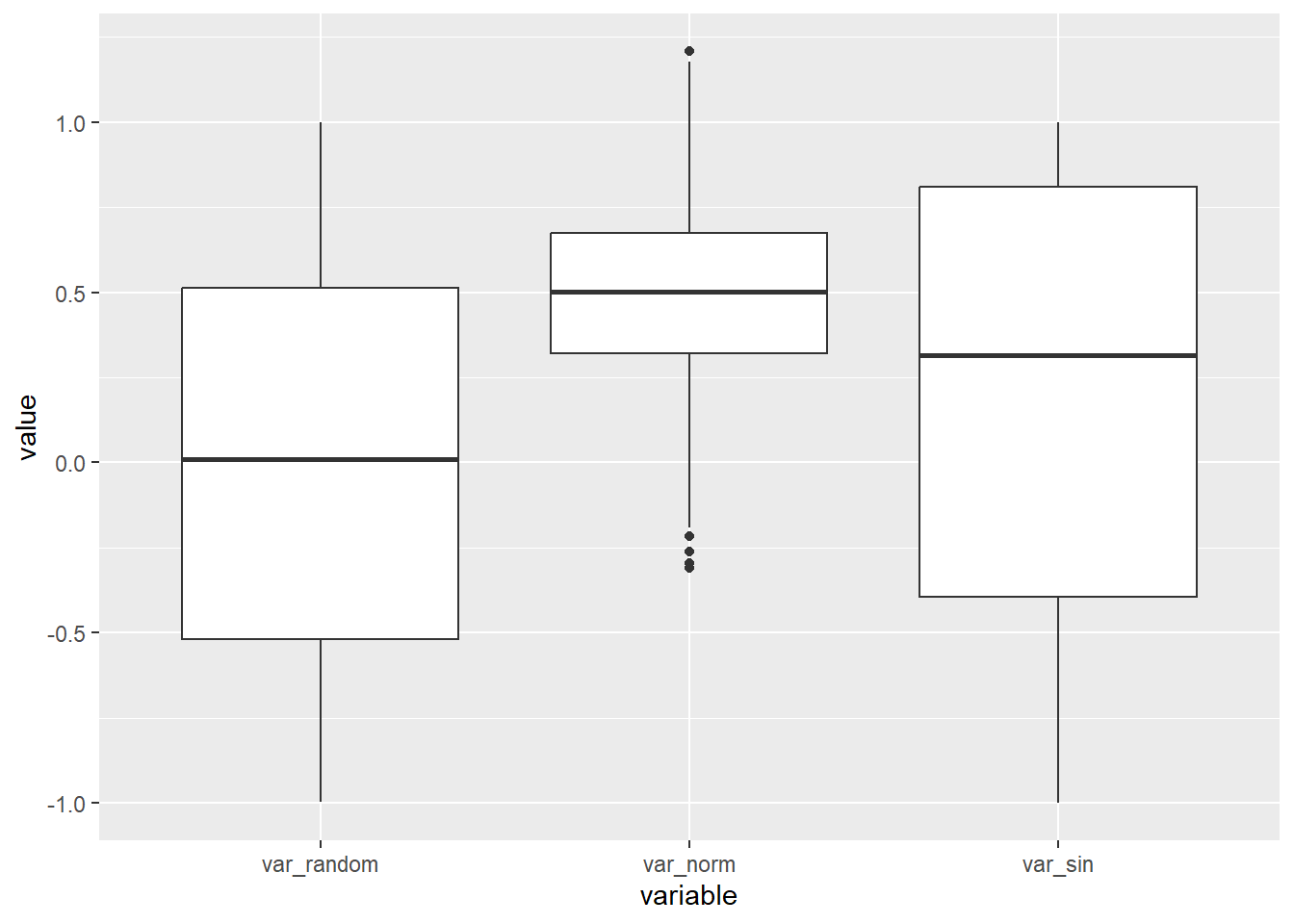

Box plots can reveal variations and central tendencies of the variables.

Pair Plots

Pair plots, or scatterplot matrices, allow us to visualize pairwise relationships between multiple variables in a dataset. They are helpful for identifying correlations and patterns among variables simultaneously. Here’s how to create a pair plot for our dataset:

library(GGally)

Registered S3 method overwritten by 'GGally':
  method from   
  +.gg   ggplot2

pair_plot <- ggpairs(dt2, columns = c("var_random", "var_norm", "var_sin", "var_sin2")) 

pair_plot

Warning in geom_point(): All aesthetics have length 1, but the data has 16 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
  a single row.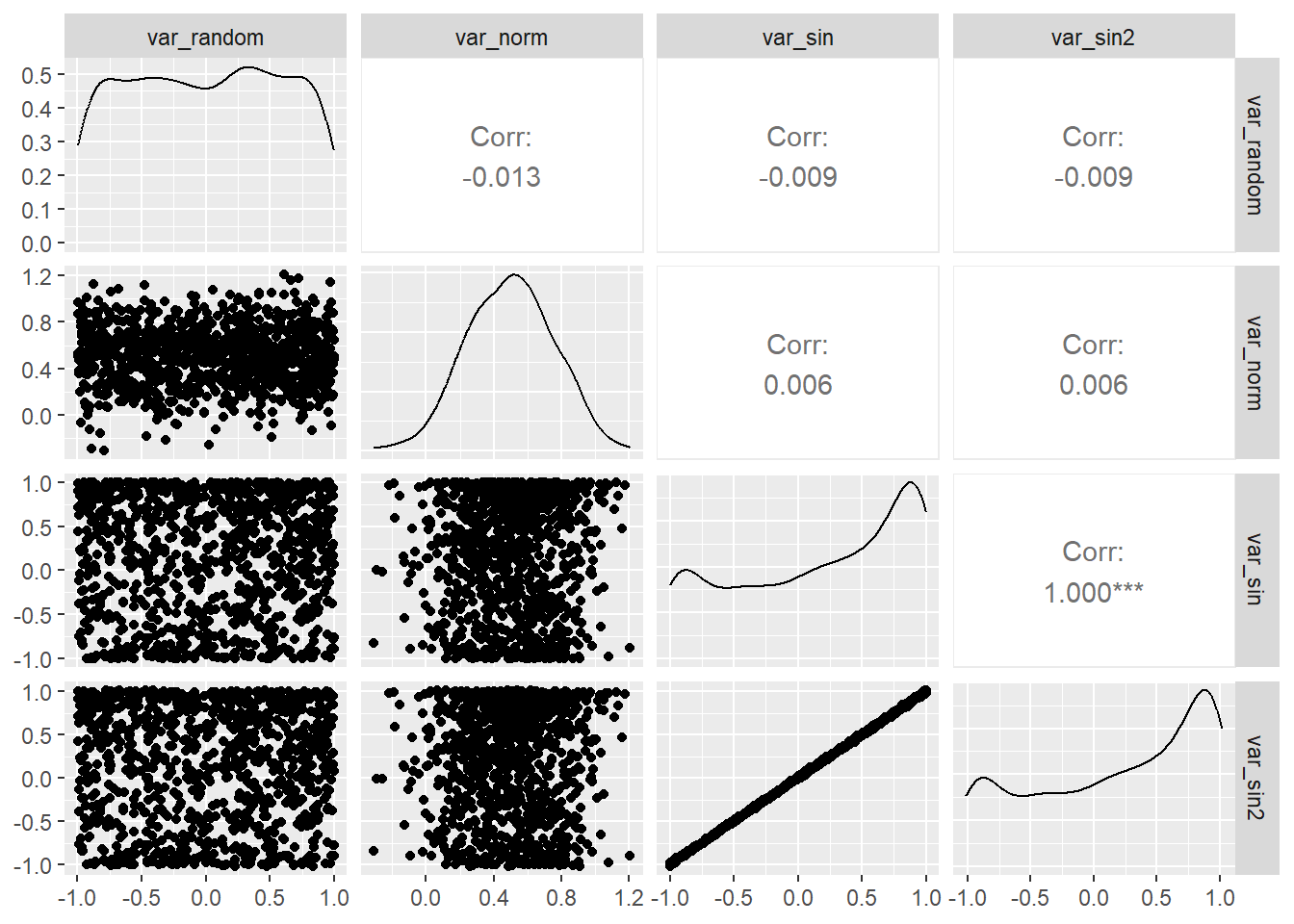

Pair plots provide a comprehensive view of variable interactions.

Time Series Decomposition

Time series data often contain underlying components such as trends and seasonality that can be crucial for understanding the data’s behavior. Time series decomposition is a technique used in Exploratory Data Analysis (EDA) to separate these components. In this section, we’ll demonstrate how to perform time series decomposition using our simulated var_sin data.

# Install and load the forecast library if not already installed
if (!requireNamespace("forecast", quietly = TRUE)) {
  install.packages("forecast")
}

Registered S3 method overwritten by 'quantmod':
  method            from
  as.zoo.data.frame zoo

library(forecast)

# Decompose the time series
sin_decomp <- decompose(ts(dt2$var_sin, frequency = 365))

# Plot the decomposed components
plot(sin_decomp)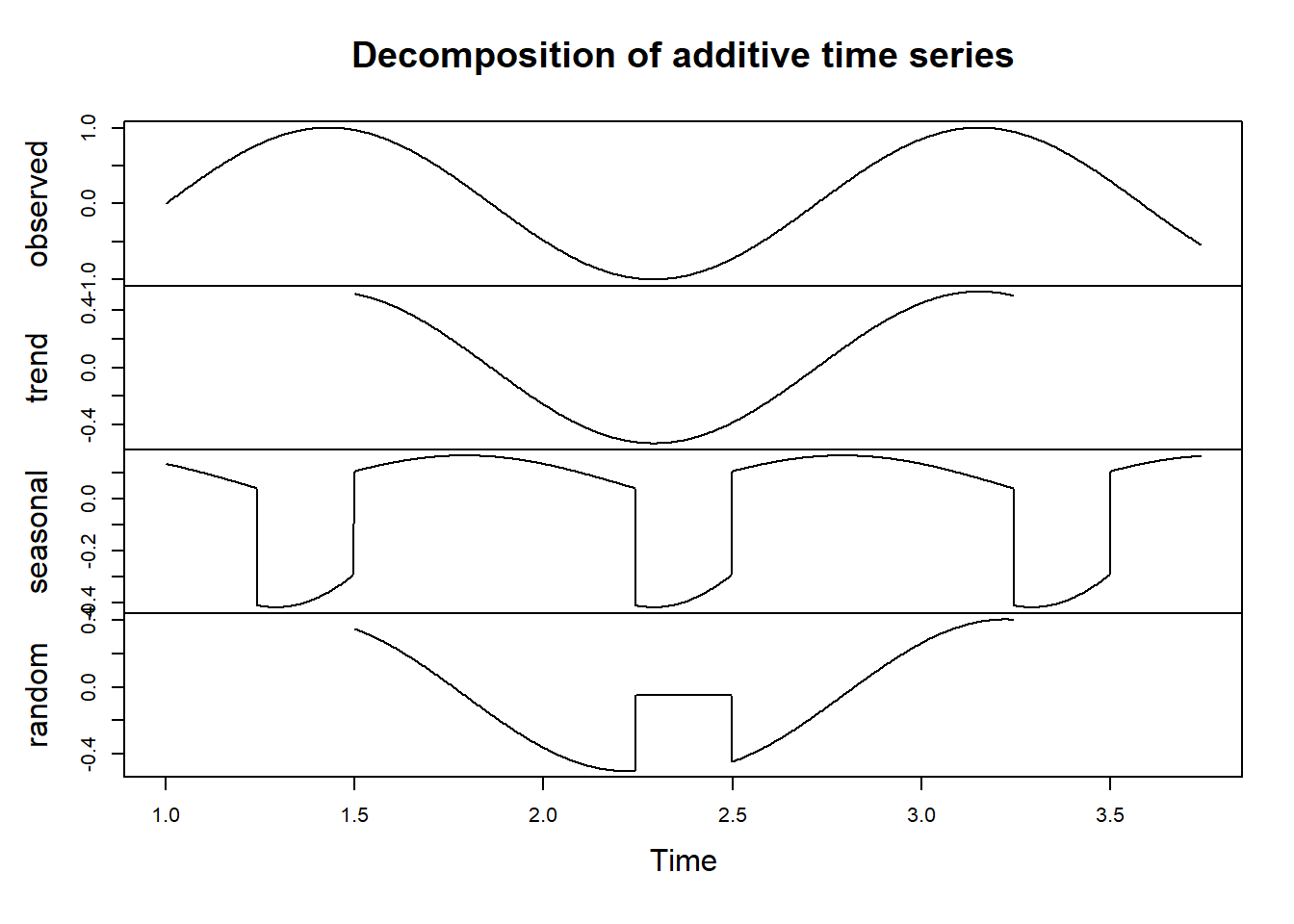

The code above performs the following:

Decomposes the var_sin time series using the decompose function. We specify a frequency of 365 since the data represents daily observations.
Plots the decomposed components, including the original time series, trend, seasonal component, and residual.

The resulting plot will show the individual components of the time series, allowing us to gain insights into its underlying patterns.

Interactive Visualizations

Interactive plots, created using libraries like plotly or shiny, allow users to explore data interactively. You can create interactive scatter plots, line plots, or heatmaps, enhancing the user’s ability to dig deeper into the data.

# Install and load the Plotly library if not already installed
if (!requireNamespace("plotly", quietly = TRUE)) {
  install.packages("plotly")
}

library(plotly)


Caricamento pacchetto: 'plotly'

Il seguente oggetto è mascherato da 'package:ggplot2':

    last_plot

Il seguente oggetto è mascherato da 'package:stats':

    filter

Il seguente oggetto è mascherato da 'package:graphics':

    layout

# Create an interactive scatter plot
scatter_plot <- plot_ly(data = dt2, x = ~var_random, y = ~var_norm, text = ~paste("x:", x, "<br>var_random:", var_random, "<br>var_norm:", var_norm),
                        marker = list(size = 10, opacity = 0.7, color = var_sin)) %>%
  add_markers() %>%
  layout(title = "Interactive Scatter Plot",
         xaxis = list(title = "var_random"),
         yaxis = list(title = "var_norm"),
         hovermode = "closest") 

# Display the interactive scatter plot
scatter_plot

In this initial section, we’ve introduced the fundamental concepts of exploratory data analysis (EDA) and the importance of data visualization in gaining insights from complex datasets. We’ve explored various types of plots and their applications in EDA.

Now, let’s dive deeper and enhance our understanding by demonstrating practical examples of EDA using real-world datasets. We’ll showcase how different types of plots and interactive visualizations can provide valuable insights and drive data-driven decisions.

Let’s embark on this EDA journey and uncover the hidden stories within our data through hands-on examples.

Examples

Time Series Decomposition for Insights

Introduction

In this section, we’ll dive into a meaningful example of time series decomposition to demonstrate its practical utility in Exploratory Data Analysis (EDA). Time series decomposition allows us to extract valuable insights from time-dependent data. We’ll use our simulated var_sin time series to illustrate its significance.

Scenario: Analyzing Daily Temperature Data

Imagine we have daily temperature data for a city over several years. We want to understand the underlying patterns in temperature variations, including trends and seasonality, to make informed decisions related to weather forecasts, climate monitoring, or energy management.

Let’s create the enhanced dataset with temperature data for multiple cities. We’ll use the data.table library to manage the dataset efficiently:

# Install and load the necessary libraries if not already installed
if (!requireNamespace("data.table", quietly = TRUE)) {
  install.packages("data.table")
}

library(data.table)

# Set the seed for reproducibility
set.seed(42)

# Generate a dataset with temperature data for multiple cities
cities <- c("New York", "Los Angeles", "Chicago", "Miami", "Denver")
start_date <- as.Date("2010-01-01")
end_date <- as.Date("2019-12-31")
date_seq <- seq(start_date, end_date, by = "day")

# Create a data.table for the dataset
temperature_data <- data.table(
  Date = rep(date_seq, length(cities)),
  City = rep(cities, each = length(date_seq)),
  Temperature = rnorm(length(date_seq) * length(cities), mean = 60, sd = 20)
)
# Filter data for New York
ny_temperature <- temperature_data[City == "New York"]

# Decompose the daily temperature time series for New York
ny_decomp <- decompose(ts(ny_temperature$Temperature, frequency = 365))

# Plot the decomposed components for New York
plot(ny_decomp)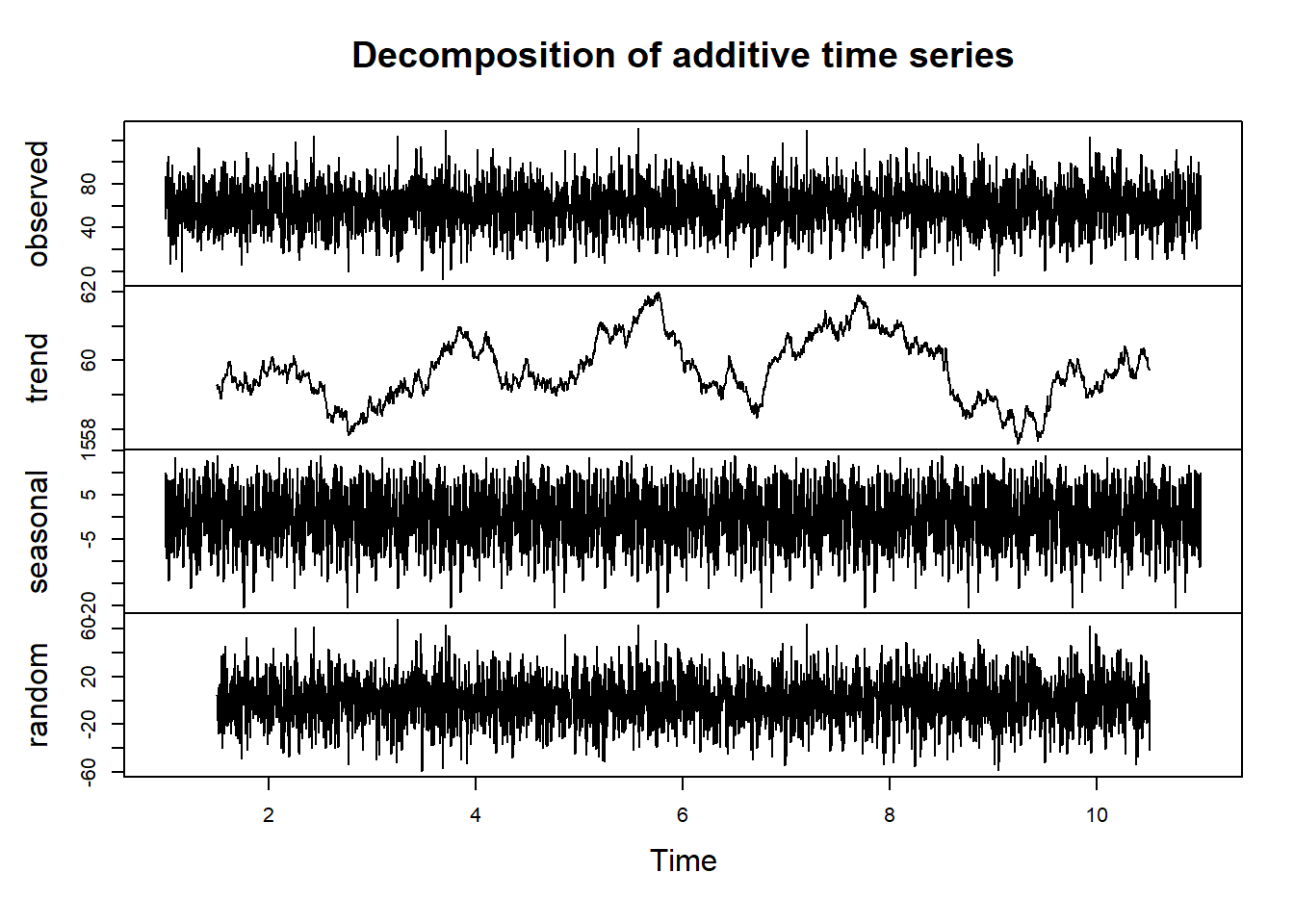

We’ve generated temperature data for each city over the span of ten years, resulting in a diverse and complex dataset.

Performing Time Series Decomposition

Now that we have our multi-city temperature dataset, let’s apply time series decomposition to analyze temperature trends and seasonality for one of the cities, such as New York (see plot)

Interpretation

The plot will display the components of the time series for New York, including the original time series, trend, seasonal component, and residual. Similar analyses can be performed for other cities to identify regional temperature patterns.

Insights and Applications

With our enhanced multi-city temperature dataset and time series decomposition, we can:

Regional Analysis: Compare temperature patterns across different cities to identify regional variations.
Seasonal Insights: Understand how temperature seasonality differs between cities and regions.
Long-Term Trends: Analyze temperature trends for each city over the ten-year period.

This advanced analysis helps us make informed decisions related to climate monitoring, urban planning, and resource management.

Leveraging Distribution Plots for In-Depth Analysis

Introduction

In this section, we’ll illustrate the significance of distribution plots in Exploratory Data Analysis (EDA) by considering a practical scenario. Distribution plots help us understand how data points are distributed and can reveal insights about the underlying data characteristics. We’ll use our simulated dataset and focus on the var_random variable.

Scenario: Analyzing Exam Scores

Imagine we have a dataset containing exam scores of students in a class. We want to gain insights into the distribution of exam scores to answer questions like:

What is the typical exam score?
Are the exam scores normally distributed?
Are there any outliers or unusual patterns in the scores?

Analyzing the Distribution of Exam Scores

Let’s create a histogram to visualize the distribution of exam scores using the var_random variable. This will help us answer the questions posed above.

# Install and load the necessary libraries if not already installed
if (!requireNamespace("ggplot2", quietly = TRUE)) {
  install.packages("ggplot2")
}

library(ggplot2)

# Create a histogram to visualize the distribution of exam scores
p3 <- ggplot(dtm[variable == "var_random"], aes(y = value, group = variable)) +
     geom_histogram(bins = 20, fill = "lightblue", color = "black", alpha = 0.7) +
     theme_minimal() +
     labs(title = "Distribution of Exam Scores",
          x = "Scores",
          y = "Frequency")

# Display the histogram
p3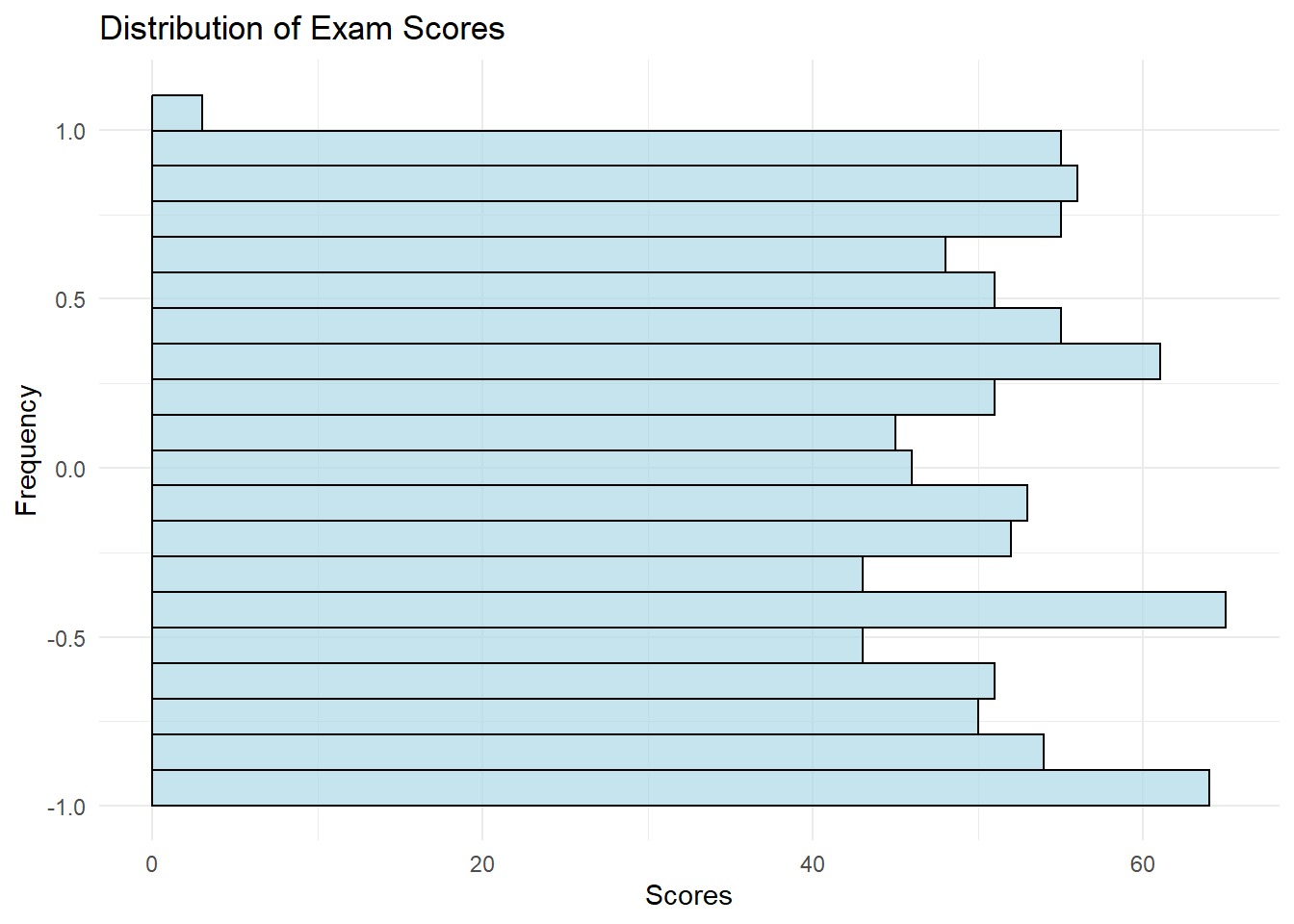

Interpretation

The resulting histogram will display the distribution of exam scores. Here’s what we can interpret:

Typical Exam Score: The histogram will show where the majority of exam scores lie, indicating the typical or central value.
Distribution Shape: We can assess whether the scores follow a normal distribution, are skewed, or have other unique characteristics.
Outliers: Outliers, if present, will appear as data points far from the central part of the distribution.

Insights and Applications

By analyzing the distribution of exam scores, we can:

Identify Central Tendency: Determine the typical exam score, which can be useful for setting benchmarks or evaluating student performance.
Understand Data Characteristics: Gain insights into the shape of the distribution, which informs us about the data’s characteristics.
Detect Outliers: Identify outliers or unusual scores that may require further investigation.

Correlation Analysis

In this section, we’ll explore advanced correlation analysis using more complex datasets. We’ll create two datasets: one representing students’ academic performance, and the other containing information about their study habits and extracurricular activities. We’ll investigate correlations between various factors to gain deeper insights.

Creating Complex Datasets

Let’s create the two complex datasets for our correlation analysis:

Academic Performance Dataset:

# Create an academic performance dataset
set.seed(123)

num_students <- 500

academic_data <- data.frame(
  Student_ID = 1:num_students,
  Exam_Score = rnorm(num_students, mean = 75, sd = 10),
  Assignment_Score = rnorm(num_students, mean = 85, sd = 5),
  Final_Project_Score = rnorm(num_students, mean = 90, sd = 7)
)

Study Habits and Activities Dataset:

# Create a study habits and activities dataset
set.seed(456)

study_data <- data.frame(
  Student_ID = 1:num_students,
  Study_Hours = rpois(num_students, lambda = 3) + 1,
  Extracurricular_Hours = rpois(num_students, lambda = 2),
  Stress_Level = rnorm(num_students, mean = 5, sd = 2)
)

Advanced Correlation Analysis

Now that we have our complex datasets, let’s perform advanced correlation analysis to explore relationships between academic performance, study habits, and extracurricular activities. We’ll calculate correlations and visualize them using a heatmap:

# Calculate correlations between variables
correlation_matrix <- cor(academic_data[, c("Exam_Score", "Assignment_Score", "Final_Project_Score")], 
                          study_data[, c("Study_Hours", "Extracurricular_Hours", "Stress_Level")])

# Install and load the necessary libraries if not already installed
if (!requireNamespace("corrplot", quietly = TRUE)) {
  install.packages("corrplot")
}

library(corrplot)

corrplot 0.92 loaded

# Create a heatmap to visualize correlations
corrplot(correlation_matrix, method = "color", type = "lower", tl.col = "black")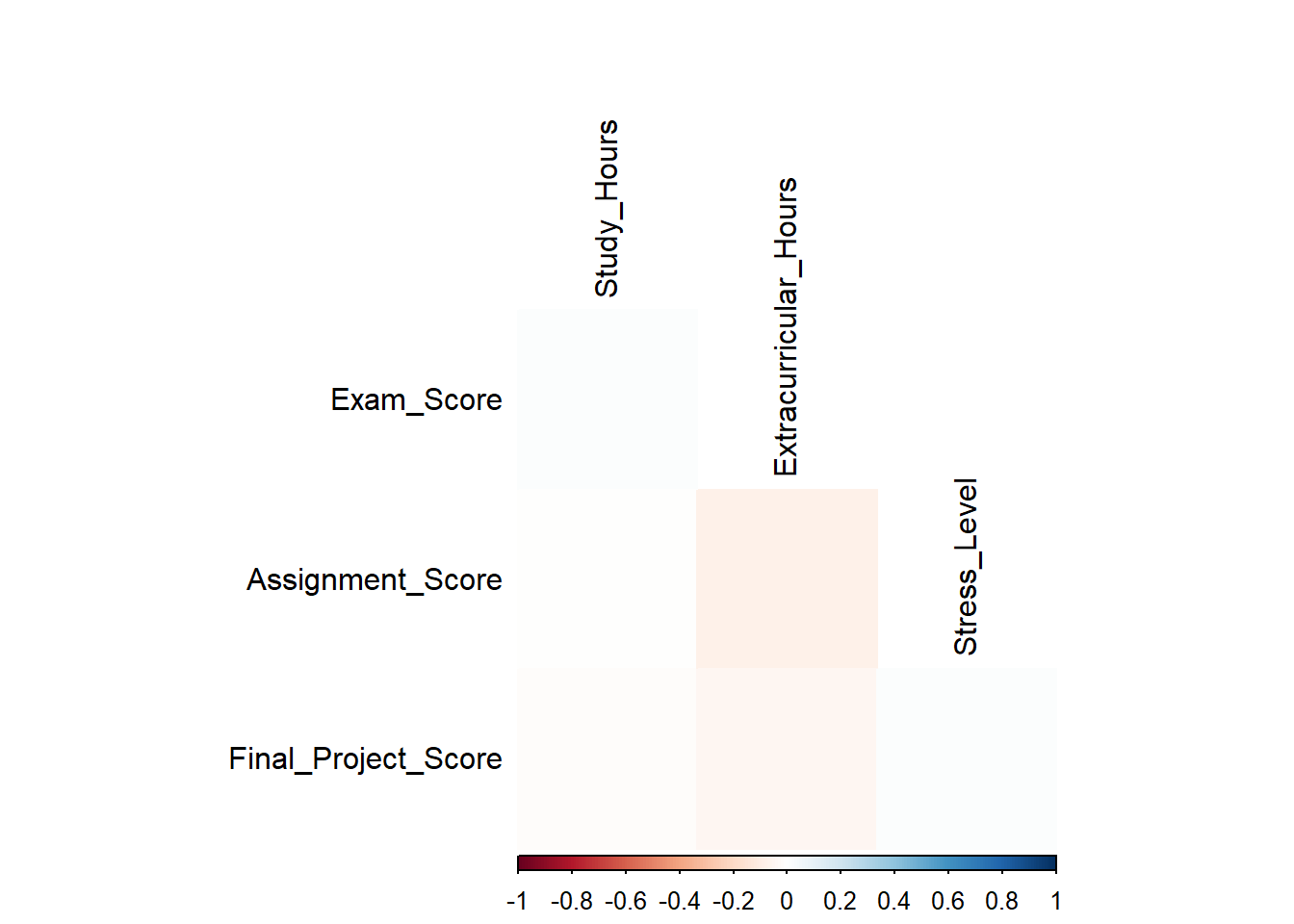

Interpretation

The resulting heatmap visually represents the correlations between academic performance and study-related factors. Here’s what we can interpret:

Color Intensity: The color intensity indicates the strength and direction of the correlation. Positive correlations are shown in blue, while negative correlations are in red. The darker the color, the stronger the correlation.
Correlation Coefficients: The heatmap displays the actual correlation coefficients as labels in the lower triangle. These values range from -1 (perfect negative correlation) to 1 (perfect positive correlation), with 0 indicating no correlation.

Insights and Applications

By conducting advanced correlation analysis, we can:

Understand Complex Relationships: Explore intricate correlations between academic performance, study hours, extracurricular activities, and stress levels.
Identify Key Factors: Determine which factors have the most significant impact on academic performance.
Optimize Student Support: Use insights to provide targeted support and interventions for students.

Advanced correlation analysis helps us uncover nuanced relationships within complex datasets.

Exploring Diverse Distributions with Box Plots

In this section, we’ll explore the versatility of box plots by working with diverse and complex datasets. We’ll create two datasets: one representing the distribution of monthly sales for multiple product categories, and the other containing information about customer demographics. These datasets will allow us to visualize various types of distributions and identify outliers.

Creating Complex Datasets

Let’s create the two complex datasets for our box plot analysis:

Sales Dataset and Customer Demographics Dataset:

# Create a sales dataset
set.seed(789)

num_months <- 24
product_categories <- c("Electronics", "Clothing", "Home Decor", "Books")

sales_data <- data.frame(
  Month = rep(seq(1, num_months), each = length(product_categories)),
  Product_Category = rep(product_categories, times = num_months),
  Sales = rpois(length(product_categories) * num_months, lambda = 1000)
)

# Create a customer demographics dataset
set.seed(101)

num_customers <- 300

demographics_data <- data.frame(
  Customer_ID = 1:num_customers,
  Age = rnorm(num_customers, mean = 30, sd = 5),
  Income = rnorm(num_customers, mean = 50000, sd = 15000),
  Education_Level = sample(c("High School", "Bachelor's", "Master's", "Ph.D."), 
                           size = num_customers, replace = TRUE)
)

# Create a box plot to visualize sales distributions by product category
p5 <- ggplot(sales_data, aes(x = Product_Category, y = Sales, fill = Product_Category)) +
     geom_boxplot() +
     theme_minimal() +
     labs(title = "Sales Distribution by Product Category",
          x = "Product Category",
          y = "Sales")

# Display the box plot
p5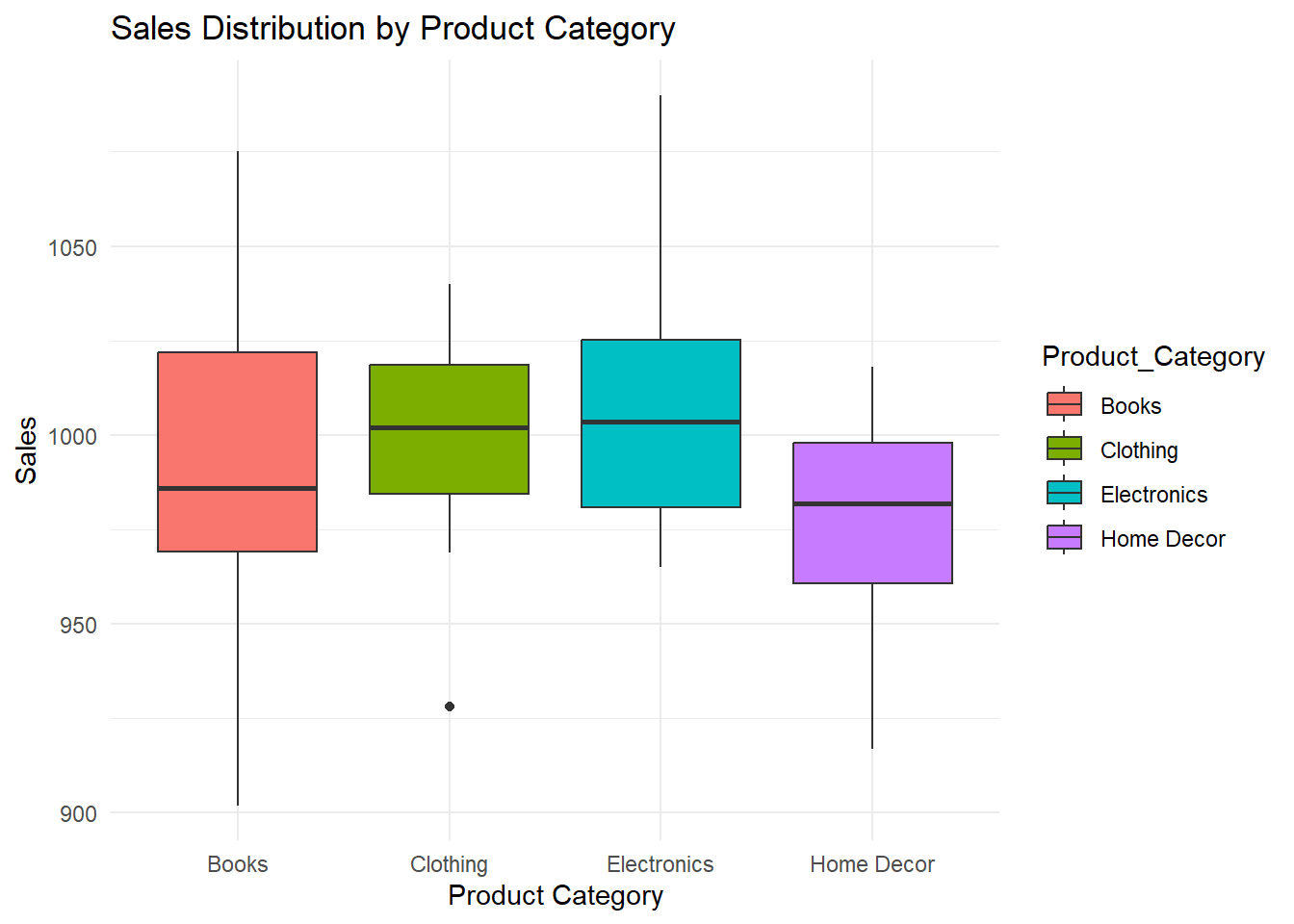

# Create a box plot to visualize the distribution of customer ages
p6 <- ggplot(demographics_data, aes(y = Age, x = "Age")) +
     geom_boxplot(fill = "lightblue", color = "black", alpha = 0.7) +
     theme_minimal() +
     labs(title = "Customer Age Distribution (Box Plot)",
          x = "",
          y = "Age")

# Display the box plot
p6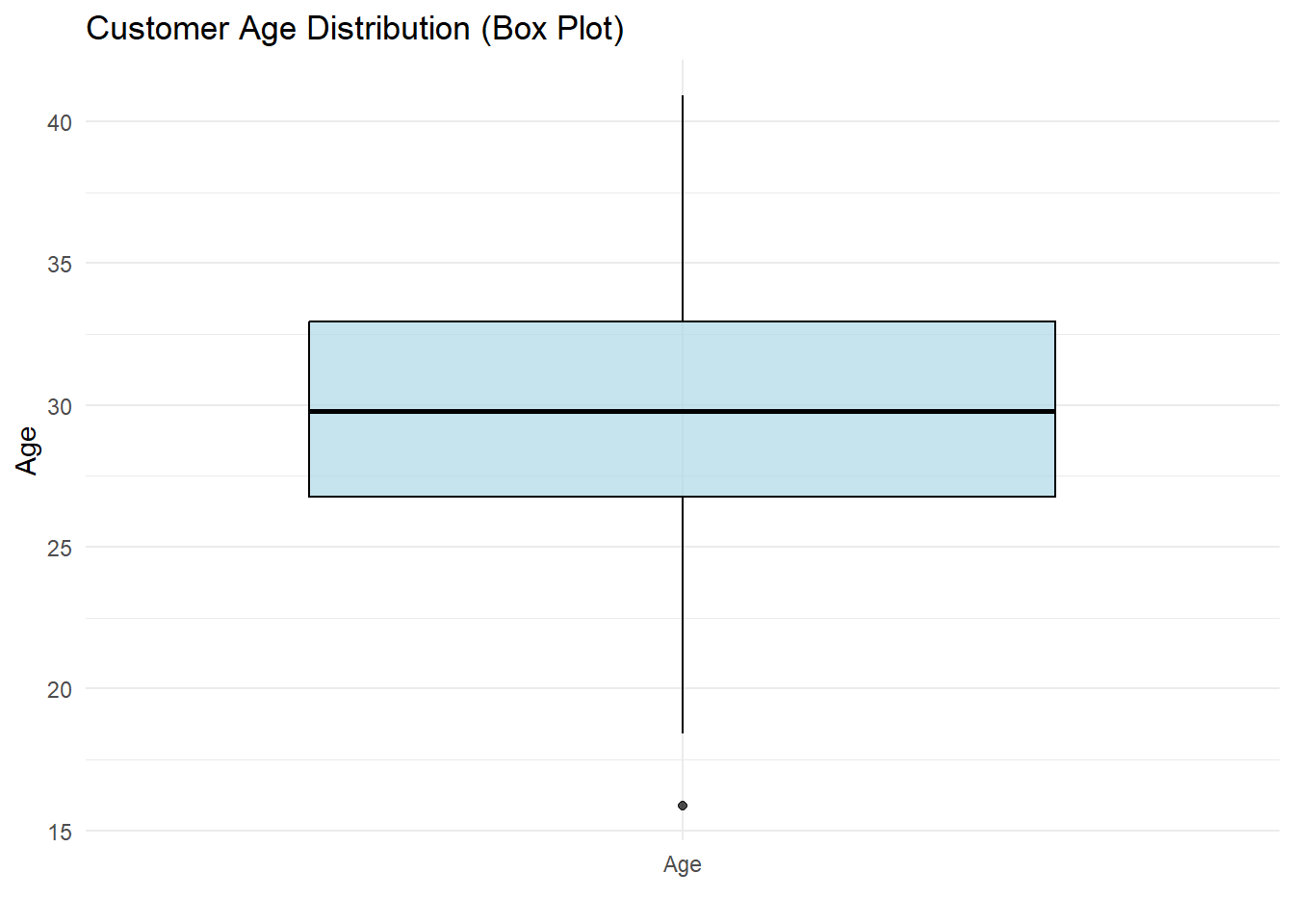

Interpretation

These box plots help us gain insights into diverse distributions:

Sales Distribution: We can observe how sales are distributed across different product categories, identifying variations and potential outliers.
Customer Age Distribution: The box plot displays the spread of customer ages, highlighting the central tendency and any potential outliers.

Insights and Applications

By using box plots with complex datasets, we can:

Analyze Diverse Distributions: Visualize and compare distributions of sales for multiple product categories and customer age distributions.
Outlier Detection: Identify potential outliers in both sales data and customer demographics.
Segmentation Insights: Understand how sales vary across product categories and the age distribution of customers.

Box plots are versatile tools for exploring various types of data distributions and making data-driven decisions.

Interactive Data Visualization with Plotly

Creating an Interactive Time Series Plot

Suppose we have a dataset containing monthly stock prices for three companies: Company A, Company B, and Company C. We want to create an interactive time series plot that allows users to:

Select the company they want to visualize.
Zoom in and out to explore specific time periods.
Hover over data points to view detailed information.

if (!requireNamespace("plotly", quietly = TRUE)) {
  install.packages("plotly")
}

library(plotly)

# Create a sample time series dataset
set.seed(789)

num_months <- 24

time_series_data <- data.frame(
  Date = seq(as.Date("2022-01-01"), by = "months", length.out = num_months),
  Company_A = cumsum(rnorm(num_months, mean = 0.02, sd = 0.05)),
  Company_B = cumsum(rnorm(num_months, mean = 0.03, sd = 0.04)),
  Company_C = cumsum(rnorm(num_months, mean = 0.01, sd = 0.03))
)

# Create an interactive time series plot with Plotly
interactive_plot <- plot_ly(data = time_series_data, x = ~Date) %>%
  add_trace(y = ~Company_A, name = "Company A", type = "scatter", mode = "lines") %>%
  add_trace(y = ~Company_B, name = "Company B", type = "scatter", mode = "lines") %>%
  add_trace(y = ~Company_C, name = "Company C", type = "scatter", mode = "lines") %>%
  layout(
    title = "Monthly Stock Prices",
    xaxis = list(title = "Date"),
    yaxis = list(title = "Price"),
    showlegend = TRUE
  )

# Display the interactive plot
interactive_plot

Interaction Features

The interactive time series plot created with Plotly offers the following interaction features:

Selection: Users can click on the legend to select/deselect specific companies for visualization.
Zoom: Users can click and drag to zoom in on a specific time period.
Hover Information: Hovering the mouse pointer over data points displays detailed information about the selected data point.

Insights and Applications

Interactive visualizations with Plotly are valuable for:

Exploration: Users can interactively explore complex datasets and focus on specific aspects of the data.
Data Communication: Presenting data in an interactive format enhances communication and engagement.
Decision Support: Interactive plots can be used in decision-making processes where users need to explore data dynamics.

Interactive data visualizations are a powerful tool for EDA and data presentation. In the next section, we’ll explore another advanced visualization technique: time series decomposition.

Interaction Features

The interactive time series plot created with Plotly offers the following interaction features:

Selection: Users can click on the legend to select/deselect specific companies for visualization.
Zoom: Users can click and drag to zoom in on a specific time period.
Hover Information: Hovering the mouse pointer over data points displays detailed information about the selected data point.

Insights and Applications

Interactive visualizations with Plotly are valuable for:

Exploration: Users can interactively explore complex datasets and focus on specific aspects of the data.
Data Communication: Presenting data in an interactive format enhances communication and engagement.
Decision Support: Interactive plots can be used in decision-making processes where users need to explore data dynamics.

[Wickham (2016)](Schloerke et al. 2021)

References

Schloerke, Barret, Di Cook, Joseph Larmarange, Francois Briatte, Moritz Marbach, Edwin Thoen, Amos Elberg, and Jason Crowley. 2021. “GGally: Extension to ’Ggplot2’.” https://CRAN.R-project.org/package=GGally.

Wickham, Hadley. 2016. “Ggplot2: Elegant Graphics for Data Analysis.” https://ggplot2.tidyverse.org.